Skip to content

XGBoost

XGBoost

XGBoost or in long version Extreme Gradient Boosting got recently very popular, especially on Kaggle competitions. It proved to outperform many other algorithms on tasks such as classification and regression. I used it few times as well and that’s why I decided to take a closer look into XGBoost to see how it works. Here’s a short summary.

Contents

XGBoost

XGBoost is a supervised learning algorithm which can be used for classification and regression tasks. It uses decision/regression trees and is based on gradient boosting technique. General idea here is to use instead of one complex model a set of simple models combined together. So that next model learns from mistakes done by the previous ones.

It is an iterative algorithm. In principle we start with some model, calculate gradient of a loss function and use this information to build next model. New model is fit on the gradient of the error from the previous prediction (hence gradient boosting). We repeat the procedure of finding next model until some fixed stopping point or when we start to overfit. We end up with set of models which when used together give much better results than every single one of them.

XGBoost is really powerful. You can find online many performance comparisons, which prove it. Let’s instead look at some of its details.

Regression

We can use XGBoost for both regression and classification.

In general we may describe extreme gradient boosting concept for regression like this:

  1. Start with an initial model F_1.

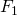This can be any model, even a constant like mean of response variables: F_1(x) = \frac{\sum_{i=1}^n y_i}{n}

  1. Calculate gradient of the loss function for results obtained from model F_1(x).
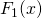    If we consider mean squared error then we get: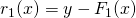 r_1(x) = y - F_1(x).
  2. Fit a regression tree model 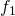f_1 using the gradient 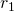r_1 as a new variable.

Now we sum up the results so our new model F2 looks like this: F_2(x) = F_1(x) + \gamma f_1(x), where \gamma is our shrinkage parameter.

  1. Repeat steps 2-3 until stop.

 

Classification

In classification task, instead of one model at each round we need to generate as many models as classes that we have. Here we look at real and predicted probability distribution in each round.

Let’s assume we have N classes.

  1. Start with N initial models: F_{11},F_{12} ..., F_{1N}.
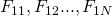  2. Calculate gradient of loss function 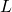L for each class for results obtained from models F_{11}(x),...,F_{1N}(x):

r_{11}(x) = \frac{\delta L}{\delta F_{11}(x)}
…
r_{1N}(x) = \frac{\delta L}{\delta F_{1N}(x)}

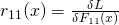
  1. Fit new decision tree models f_{11}, f_{12}, ..., f_{1N} to obtained gradients.

Sum up results to get new models: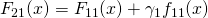
F_{21}(x) = F_{11}(x) + \gamma_1 f_{11}(x),
…
F_{2N}(x) = F_{1N}(x) + \gamma_N f_{1N}(x),

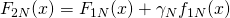where 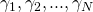\gamma_1, \gamma_2, ..., \gamma_N are shrinkage parameters.

  1. Repeat steps 2-3 until stop.

 

Loss function

As in any machine learning case our goal is to minimise a loss function. In XGBoost we can use any loss function we want. The most typical one for regression is the mean squared error (MSE):

L(y, F_i(x)) = (y-F_i(x))^2

where F_i is a model that we apply in a given round.

Then if we calculate gradient of this function:

\frac{\delta L(y, F_i(x))}{\delta F_i(x))} = -2(y - F_i(x))

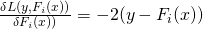
we can see that we actually need to minimise the residuals: y - F_i(x), which makes MSE very intuitive to use.

For classification we may for example consider KL-divergence as loss function. It takes into consideration difference between two probability distributions. For each class we look at the true probability distribution and the one predicted by some model.

 

Shrinkage

While building next models we use so called shrinkage parameter, which 0 < \gamma < 1. It is also called learning rate, as in general it determines how many models we’ll use in the end. This parameter prevents overfitting by adjusting too much to the actual results. Generally the smaller it is, the better the performance and longer training time.

 

Stopping

At some point we need to stop adding yet new models. Either we may assume some maximal number of models we want to produce (like 1000) and adjust it if needed. Or we can use cross-validation technique and stop at point when we start getting with each iteration worse results on testing set (with each iteration we adjust more to training set).

 

The Extreme part

While finding the best tree model for each round we need to determine the best feature split. Normal gradient boosting is a greedy algorithm, which considers and leverages all possible splits. XGBoost is tweaked in such a way so that it just searches through subset of splits. It first looks at the distribution of the data features and then specifies the possible best splits to be verified. That significantly speeds up the processing.

 
While working with XGBoost we also need to specify some other parameters, like maximal depth of the tree or minimal tree split.

Not only performance is a big advantage of XGBoost. It also nicely handles high dimensional and sparse data.

In R you may find it embedded in xgboost package.

«
»

Leave a Reply

Your email address will not be published. Required fields are marked *